Disciplina: Matemática 0 Curtidas

Em um parque há dois mirantes de alturas distintas que são - Enem 2017

Em um parque há dois mirantes de alturas distintas que são acessados por elevador panorâmico. O topo do mirante 1 é acessado pelo elevador 1, enquanto que o topo do mirante 2 é acessado pelo elevador 2. Eles encontram-se a uma distância possível de ser percorrida a pé, e entre os mirantes há um teleférico que os liga que pode ou não ser utilizado pelo visitante.

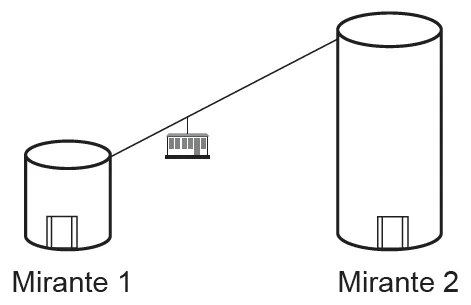
O acesso aos elevadores tem os seguintes custos:

• Subir pelo elevador 1: R$ 0,15;
• Subir pelo elevador 2: R$ 1,80;
• Descer pelo elevador 1: R$ 0,10;
• Descer pelo elevador 2: R$ 2,30.

O custo da passagem do teleférico partindo do topo do mirante 1 para o topo do mirante 2 é de R$ 2,00, e do topo do mirante 2 para o topo do mirante 1 é de R$ 2,50.

Qual é o menor custo, em real, para uma pessoa visitar os topos dos dois mirantes e retornar ao solo?

1. 2,25

2. 3,90

3. 4,35

4. 4,40

5. 4,45

Solução