Disciplina: Matemática 0 Curtidas
Seja FGV um triângulo isósceles, desenhado no plano - FGV 2020
Seja FGV um triângulo isósceles, desenhado no plano cartesiano de eixos ortogonais, com FG = GV = 5 e FV = 6, vértice F coincidindo com a origem dos eixos, FV contido no eixo x e ângulos internos, em radianos, como mostra a figura 1.
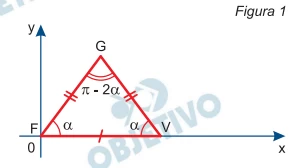
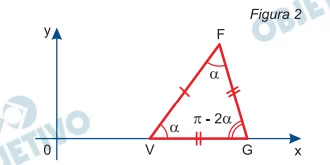
O mesmo procedimento é repetido, agora com centro em G, até que GF fique contido no eixo x, e assim sucessivamente.
Partindo da situação descrita na figura 1 e fazendo 30 giros com a regra estabelecida, o deslocamento do ponto F, em unidades do plano cartesiano, será igual a
-
20(3π + 2α)
-
60(π + α)
-
60(π + 2α)
-
30(2π + α)
-
10(2π + 3α)
Solução
Alternativa Correta: A) 20(3π + 2α)
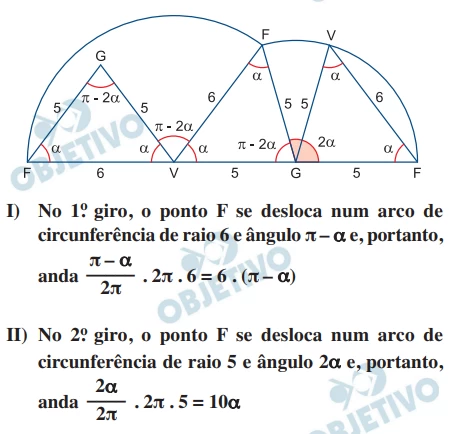III) No 3o . giro, o ponto F não se desloca.
Assim, em 30 giros ele se desloca
10 . (6 . (π – α) + 10α) =
= 10 . (6π + 4α) = 20 . (3π + 2α)
Resolução adaptada de: Curso Objetivo
Institução: FGV
Ano da Prova: 2020
Assuntos: Geometria Plana
Vídeo Sugerido: YouTube