Disciplina: Matemática 0 Curtidas

Um triângulo isósceles ABC, com AB = AC = 1, é tal que - FGV 2018

Um triângulo isósceles ABC, com AB = AC = 1, é tal que cada ângulo da base BC mede o dobro do ângulo de vértice A.

Se cos18º = m, então, o quadrado de BC é igual a

1. 2(1 + m – √1 – m²)

2. 2(1 – m +√1 – m² )

3. 2 – 2m²

4. 4 – 2m²

5. 4 – 4m²

Solução

Alternativa Correta: E) 4 – 4m²

A partir das informações do texto, podemos montar a seguinte figura, onde x é a medida do ângulo de vértice A.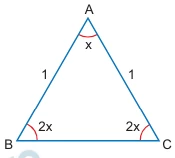

Assim, temos:
x + 2x + 2x = 180°
x = 36°
Utilizando a lei dos cossenos no triângulo ABC, temos:
BC2 = 1² + 1² – 2 . 1 . 1 . cos 36° (I)
Como cos 18° = m e cos 2θ = 2 . cos²θ – 1, temos:
cos 36° = 2 . cos² 18° – 1
cos 36° = 2 m² – 1 (II)
Substituindo II em I, temos:
BC2 = 1 + 1 – 2 . (2m² – 1)
BC2 = 2 – 4m² + 2
BC2 = 4 – 4m²

Resolução adaptada de: Curso Objetivo

Gostei Não Gostei

Ajude-nos com uma doação!

Nós trabalhamos duro para manter este site e oferecer conteúdo de qualidade gratuitamente. Se você gostou do que oferecemos, por favor, considere fazer uma doação de qualquer valor através do PIX para nos ajudar a manter o site funcionando. Sua contribuição é muito valiosa para nós!
Chave PIX: contato@estudaporaqui.com.br
Recebedor: Wesley Rodrigues

Institução: FGV

Ano da Prova: 2018

Assuntos: Relações Métricas em Triângulos

Vídeo Sugerido: YouTube