Disciplina: Raciocínio Lógico 0 Curtidas
FGV - Considere a matriz e seja n um número natural
Considere a matriz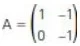 
e seja n um número natural maior que 1. Na matriz A2n , o elemento que ocupa a 1ª linha e 2ª coluna é:
-
–1.
-
0.
-
1.
-
n
-
2n
Solução
Alternativa Correta: B) 0.
Podemos reescrever a matriz A para da seguinte maneira (A^2)^n= A^2n
Se resolver a matriz A^2
AxA = 1 -1 x 1 -1 = 1*1 + (-1*0) ___1*(-1)+ (-1)(-1) = 1 0 = I
______0 -1 _0 -1 ___0*1 +(-1)*0 ____0*(-1)+(-1)*(-1) _0 1
O Resultado da multiplicação da matriz A^2 é a matriz identidade. Qualquer que seja o valor N o resultado sempre será a matriz identidade.
Logo o elemento Aij = A12 = 0
Resolução adaptada de: QConcursos
Banca Examinadora: FGV
Ano da Prova: 2009
Assuntos: Matrizes
Vídeo Sugerido: YouTube