Disciplina: Matemática 0 Curtidas
Os menores lados de uma folha de papel retangular de - UNESP 2018/2
Os menores lados de uma folha de papel retangular de 20 cm por 27 cm foram unidos com uma fita adesiva retangular de 20 cm por 5 cm, formando um cilindro circular reto vazado.
Na união, as partes da fita adesiva em contato com a folha correspondem a dois retângulos de 20 cm por 0,5 cm, conforme indica a figura.
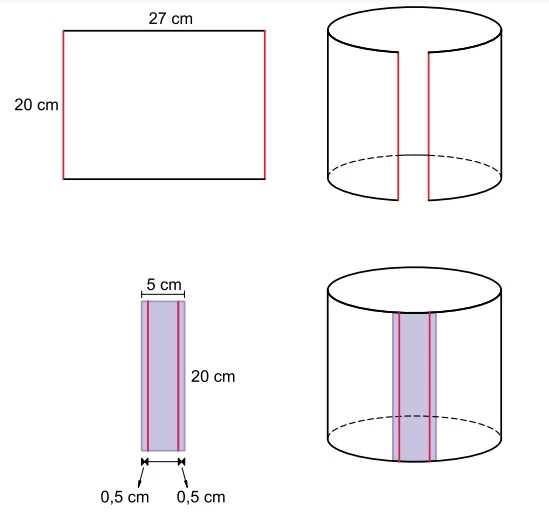
Desprezando-se as espessuras da folha e da fita e adotando π = 3,1, o volume desse cilindro é igual a
-
1 550 cm3.
-
2 540 cm3.
-
1 652 cm3.
-
4 805 cm3.
-
1 922 cm3.
Solução
Alternativa Correta: A) 1 550 cm3.
Sendo R, em centímetros, o raio da base do cilindro, temos:
2 . π . R = 27 + 5 – 0,5 – 0,5
2 . 3,1 . R = 31 ⇔ R = 5
Logo, o volume V desse cilindro com raio da base
R = 5 cm e altura h = 20 cm é igual a
V = π . R2 . h = 3,1 . 52 . 20 ⇔ v = 1550 cm3.
Resolução adaptada de: Curso Objetivo
Institução: UNESP
Ano da Prova: 2018
Assuntos: Volume do Cilindro
Vídeo Sugerido: YouTube