Disciplina: Outras Disciplinas 0 Curtidas

A posição dos polos é determinante para verificar a estabilidade

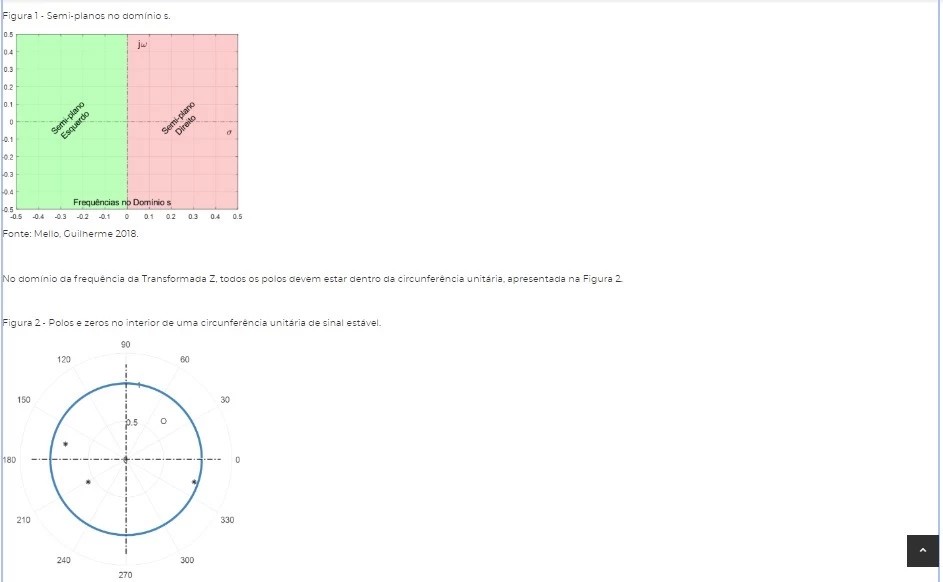
A posição dos polos é determinante para verificar a estabilidade de sistemas dinâmicos. No domínio da frequência de Laplace, todos os polos devem estar no semi-plano esquerdo, como apresentado na Figura 1 para se determinar estabilidade.

Figura 1 - Semi-planos no domínio s.

Semi-planos direito e esquerdo.

Fonte: Mello, Guilherme 2018.

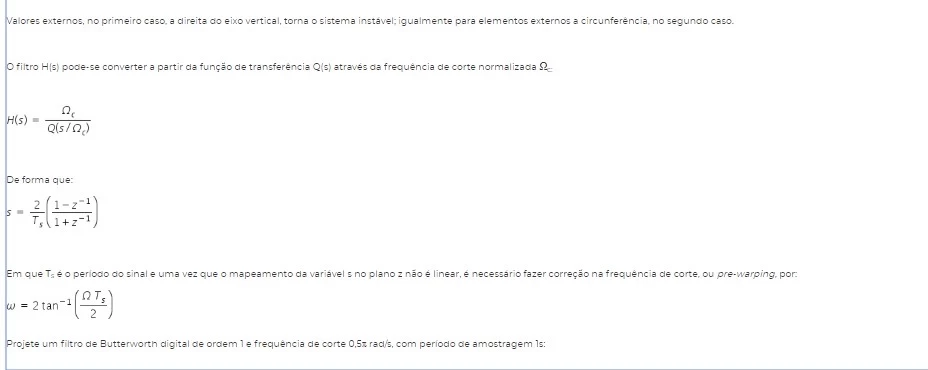
No domínio da frequência da Transformada Z, todos os polos devem estar dentro da circunferência unitária, apresentada na Figura 2.

Figura 2 - Polos e zeros no interior de uma circunferência unitária de sinal estável.

Transformada Z - CircUnitário

Fonte: Mello, Guilherme 2018.

Valores externos, no primeiro caso, a direita do eixo vertical, torna o sistema instável; igualmente para elementos externos a circunferência, no segundo caso.

O filtro H(s) pode-se converter a partir da função de transferência Q(s) através da frequência de corte normalizada Ωc:

H left parenthesis s right parenthesis space equals space fraction numerator capital omega subscript c over denominator Q left parenthesis s divided by capital omega subscript c right parenthesis end fraction

De forma que:

s space equals space 2 over T subscript s open parentheses fraction numerator 1 minus z to the power of negative 1 end exponent over denominator 1 plus z to the power of negative 1 end exponent end fraction close parentheses
Em que Ts é o período do sinal e uma vez que o mapeamento da variável s no plano z não é linear, é necessário fazer correção na frequência de corte, ou pre-warping, por:
omega space equals space 2 space tan to the power of negative 1 end exponent space open parentheses fraction numerator capital omega space T subscript s over denominator 2 end fraction close parentheses
Projete um filtro de Butterworth digital de ordem 1 e frequência de corte 0,5π rad/s, com período de amostragem 1s:

Solução